Comprehensive Exam Notes
Questions for Kwiatkowska2011 (Stochastic Model Checking)
Q1-a-ii
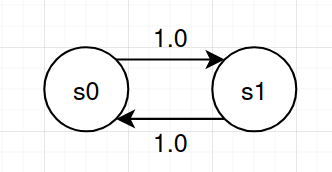
After further discussion, it is clear that the steady state operator is not equivalent to the transient unbounded until operator. This is because the transient unbounded until operator represents a path probability, and its analysis terminates after reaching a post-until satisfying state. For example, in the following 2-state DTMC, the steady-state (S=?) probability at either state is 1/2, since there is a 50% chance of being in either state in the long run. However, there is a 100% chance to end up in either state within unbounded time steps, so the transient (P=?) probability at either state is 1.
Questions for Baier2003 (Model Checking Algorithms)
Q2-b
The formulas are not actually equivalent. Consider a model $\mathcal{M}$ where only the initial state satisfies $\varphi$. That is, $s_0 \models \varphi$, but $\forall i \neq 0 \cdot s_i \not \models \varphi$.
Because $P$ is used to represent the transient probability, if the initial state satisfies $\varphi$, the probability of reaching a state satisfying $\varphi$ is 1. In other words, $\mathcal{M} \models P_{\geq 1}(\varphi)$, and the CSL formula holds.
The CTL formula, however, requires that for all paths starting at $s_0$, $\varphi$ must hold. If only $s_0$ satisfies $\varphi$, then the model transitions to a state not satisfying $\varphi$, $\mathcal{M} \not \models \forall \varphi$.
This state space is a counterexample to the claim $\mathcal{M} \models \forall \varphi \iff \mathcal{M} \models P_{\geq 1}(\varphi)$, so the claim is not true.
Q2-d
Consider by contradiction that $s \models \Phi$ is sufficient for Case 3. This creates the following problems:
- The glaring problem is that there would be ambiguity between Case 2 and Case 3. If $s \models \Phi \land \lnot \Psi$, it is not clear whether Case 2 or Case 3 should be selected. Because of the inclusion of the exponential function in Case 3, the formulas are not equivalent, and this creates a conflict in the evaluation of the formula.
- Neglecting ambiguity, if Case 3 were to be applied when $s \models \Phi \land \lnot \Psi$, we would erroneously be including the exponential function, representing the probability of staying in a pre-until state for $x$ time units, where $x \leq a$.
Questions for Batz2020 (PrIC3)
Q3-a
My slides and other details are available at https://docs.mossbiscuits.com/pdr/
In response to the clarifying questions:
A frame $F_k$ (assuming we’re discussing traditional PDR for Boolean systems) is a set of clauses representing an overapproximation of all the states that can be reached in $k$ steps. For example, the formula for frame $F_3$ includes all states reachable from an initial state in $3$ steps. A frame is constructed by the following:
- Overapproximate the reachable area, potentially by setting frame $F_k$’s formula to $\texttt{true}$ to include all states.
- Attempt to “block” bad states by excluding them in the formula for $F_k$. For example, if a bad state is represented by $x \lor y$, the new formula may be $\texttt{true} \land \lnot (x \lor y)$.
- Perform single-step invariant checking on the new formula (i.e., check one step from $F_{k-1}$ to $F_k$. If the model can reach the blocked region in $F_k$ from $F_{k-1}$, recursively go back to $F_{k-1}$ to attempt blocking bad states, until reaching $F_0$.
- If at $F_0$, you cannot block regions that eventually lead to a bad state, the bad state is reachable, and it is possible to provide a counterexample to the user.
- Keep adding frames representing one additional step in the transition system. If the last two frames become identical after attempting to block regions that reach bad states, we know that we have explored the entirety of the reachable state space (i.e., we know that we cannot take one step to reach any state outside the un-blocked regions). The final overapproximation of the reachable states is returned to the user as an inductive invariant, which proves the bad states are unreachable.
Current Research
I’m focused on 3 main topics right now:
State Representation. We recently submitted a paper to CAV proposing the use of a prefix tree to save memory in very large explicit state spaces for probabilistic model checking.
Provably correct Rust tool implementations. We are implementing our group’s tools (including Ragtimer, Wayfarer, and Stamina) in Rust in a provably correct way. We have seen promising results after implementing a dependency graph for VAS analysis.
Applications of SMT & PDR for probabilistic models. We’ve been using BMC to find potential bounds for variables (to reduce the size of state spaces). We are curious about the potential to use PDR methods to approximate probabilities for regions of a state space for CTMCs, to help with the intractibly large state space problem.